Quantcast
Channel: mathcounts notes
Viewing all 242 articles
Browse latest View live
↧

2015 AMC-8 prep

September 4, 2015, 7:51 am
$
0
0
Hi,
Thanks a lot for visiting my blog.

E-mail me at thelinscorner@gmail.com if you want to join us who LOVE problem solving (and many other areas equally challenging and engaging.)

Currently I'm running different levels of problem solving group lessons.Our first stop is AMC 8 and/or the SAT hardest problems prep (just for the very short term for a full ride scholarship).

Come join the fun !!  Take care and cheers, Mrs. Lin

Unofficial , official problems, answer key and detailed solutions to 2014 AMC8 test + official statistics.


This year's (2013) AMC-8 results can be viewed here.

2013 AMC-8 problems in pdf format (easier to print out and work on it as a real test)

Try this if your school doesn't offer AMC-8 test.
40 minutes without a calculator.

If you want to use the test to prepare for Mathcounts, cover the multiple choice
options to make the questions harder unless you have to see the choices to answer
the question(s) asked.

2013 AMC-8 problems

2013 AMC-8 answer key

2013 AMC-8 problems with detailed (multiple) solutions 

Trickier problems : #18, 21(mainly the wording) and maybe 25 (slightly tricky)

2014 AMC-8 Result Statistics can be viewed here.

2014 AMC-8 problems and solutions from AoPS wiki. 

Comments :

#4 : We've been practicing similar problems to #4 so it should be a breeze if you see right away that the prime number "2" is involved. You'll get a virtual bump if you forgot about that again.

 #10 : Almost every test has this type of problem, inclusive, exclusive, between, calendar, space, terms, stages... It's very easy to twist the questions in the hope of confusing students, so slow down on this type of question or for the trickier ones, skip it first. You can always go back to it if you have time left after you get the much easier-to-score points.  (such as #12, 13, 18 -- if you were not trolled and others)

 #11 : Similar questions appear at AMC-10, Mathcounts.  For harder cases, complementary counting is easier.
This one, block walk is easier.



 #12: 1/ 3!

How about if there are 4 celebrities ? What is the probability that all the baby photos match with the celebrities ? only 1 baby photo matches,  only2 baby photos match, 3 baby photos match, or none matches ?

 #13: number theory

For sum of odd and /or even, it's equally likely --
odd + odd = even ; even + even = even
odd + even = odd ; even + odd = odd

For product of odd and/or even, it's not equally likely --
odd * even = even ; even * even = even
odd * odd = odd

For product probability questions, complementary counting with total minus the probability of getting odd product (all odds multiply)is much faster.

SAT/ACT has similar type of problems.

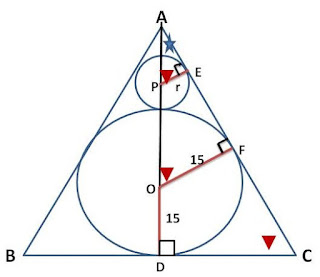
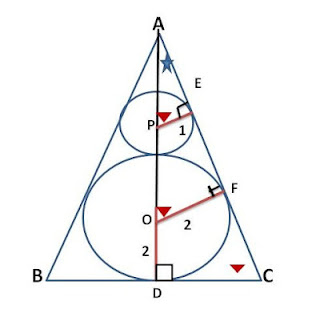
#15 : Central angle and inscribed angles --> Don't forget radius is of the same length.
Learn the basics from Regents prep 

#17: rate, time and distance could be tricky

Make sure to have the same units (hour, minutes or seconds) and it's a better idea writing down
R*T = D so you align the given infor. better.

Also, sometimes you can use direct/inverse relationship to solve seemingly harder problems in seconds.

 Check out the notes from my blog and see for yourself.

#18 : Trolled question. Oh dear !! 

1 4 6 4 1     , but it doesn't specify gender number(s) so 
(4 + 4)/2^4 is the most likely. 

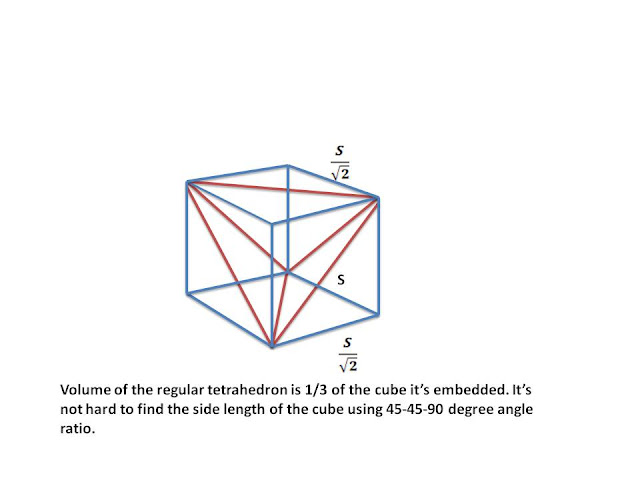
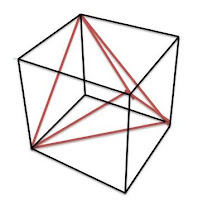
#19 : more interesting painted cube problems --> one cube is completely hidden inside.

Painted cube animation from Fairy Math Tutors

Painted cube review   Use Lego or other plops to help you visualize how it's done.


#20 : Use 3.14 for pi and if you understand what shape is asked, it's not too bad.

#21: You can cross out right away multiples of three or sum of multiples of 3 by first glance.
For example 1345AA, you can cross out right away 3 and 45 (because 4 + 5 = 9, a multiple of 3).
You don't need to keep adding those numbers up. It's easier this way.

#22 : To set up two-digit numbers, you do 10x + y.
To set up three-digit numbers, you do 100x + 10y + z 

For those switching digits questions, sometimes faster way is to use random two or three digit numbers, not in this case, though.

#23 : This one is more like a comprehension question. Since it relates to birthday of the month, there are not many two digit primes you need to weight, so 11, 13 and 17. (19 + 17 would exceed any maximum days of the month). From there, read carefully and you should get the answer.

#24 : a more original question --

To maximize the median, which in this case is the average of the 50th and 51st term, you minimized the first 49 terms, so make them all 1s.
Don't forget the 51st term has to be equal or larger than the 50th term.

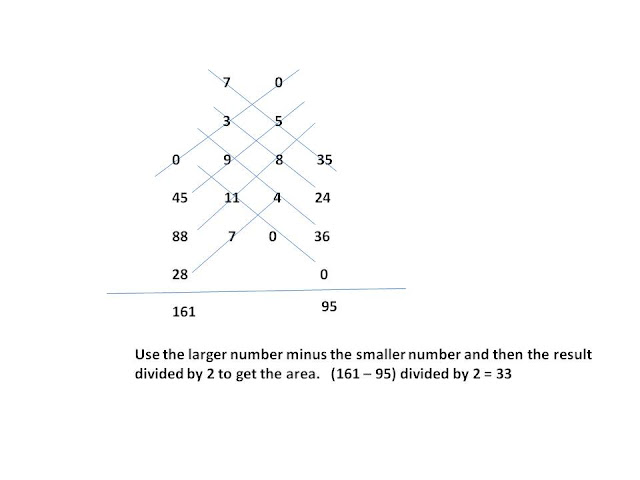
#25: The figure shown is just a partial highway image. 40 feet is the diameter and the driver's speed is 5 miles per hour, so units are not the same --> trap

I've found most students, when it comes to circular problems, tend to make careless mistakes because there are just too many variables.
Areas, circles, semi-circles, arch, wedge areas, and those Harvey like "think outside the box" fun problems.

Thus, it's a good idea to slow down for those circular questions. Easier said than remembered.

Happy Holiday !!


↧
Search

Original Problem from a Student Problem Solver on Similar Triangles

September 12, 2015, 2:35 pm
$
0
0
An original problem on similar triangles from Varun (from FL)

↧
↧

2013 Mathcounts State Prep : Geometry Quetsions

February 3, 2015, 9:40 am
$
0
0



Find the sum of the area of the two shaded regions. (or lunes)        









Solution:
The area of the two shaded regions (or lunes) combined = the area of the right triangle

Proof:
If the base of a triangle in a circle is the diameter, the triangle is a right triangle.

The area of the right triangle is 2a * 2 b over 2 or 2ab
The area of the two lunes = \(\dfrac {\left( a^{2}+b^{2}\right) \pi }{2}\) - [\(\dfrac {c^{2}\pi } {2}-2ab\)]
=  \(\dfrac {c^{2}\pi } {2}\) - \(\dfrac {c^{2}\pi } {2}+ 2ab\) = 2ab = the area of the right triangle

\(a^{2}+b^{2}=c^{2}\) because of the Pythagorean theorem.







Fine the area of the shaded region. (lune)

Solution:
Usually the diameter or radius is given as well as the length of line AB, which in this case is the diameter of the small semi circle.

From given, it's easy to see if AOB is an equilateral, 30-60-90 or 45-45-90, etc triangle.

Use the area of the small semi-circle minus [the arch area of arch ABO minus triangle ABO], you'll get the area of the lune.

 More links to explore :

 Area of a Lune by Jim Wilson

Another way of solving the above question by Jim Wilson
↧

2015 Mathcounts State Prep : Inscribed Cricle Radius and Similar Triangles

October 13, 2015, 5:18 am
$
0
0



Question : \(\Delta\) ABC is an equilateral triangle. Circle "O" is the inscribed circle and it's radius is 15. 

What is the length of the radius of the smaller circle p which is tangent to circle "O" and the two sides?








Here is the link to the basics of inscribed circle radius as well as circumscribed circle radius of an equilateral triangle.

Solution I :
The length of the radius of an inscribed circle of an equilateral triangle is \(\dfrac {1} {3}\) of the height so you know AO is \(\dfrac {2} {3}\) of the height or 30 (the height is 15 + 30 = 45 unit long)

\(\Delta\) AEP is similar to \(\Delta\) AFO \(\rightarrow\) \(\dfrac {r} {15}=\dfrac {AP} {30}\)
so \(\overline {AP}\) = 2r.
\(\overline {AP}+\overline {PO}=30\)  \(\rightarrow\)2r + r + 15 = 30   \(\rightarrow\)  3r = 15 so r = 5 
or \(\dfrac {1} {3}\) of the larger radius 

Solution II:
\(\Delta\) APE is a 30-60-90 right triangle, so \(\overline {AP}\) = 2r
\(\overline {PO}\) = r + 15
\(\overline {AP}+\overline {PO}\)  \(\rightarrow\)  2r + r + 15 = 30  \(\rightarrow\)  3r  =  15 so  r  = 5 
or \(\dfrac {1} {3}\) of the larger radius 



This is an AMC-10 question.

\(\Delta\) ABC is an isosceles triangle.

The radius of the smaller circle is 1 and the radius of the larger circle is 2,

A: what is the length of \(\overline {AP}\) ?

B. what is the area of \(\Delta\) ABC?







Solution for question A: 
\(\Delta\) AEP is similar to \(\Delta\) AFO \(\rightarrow\) \(\dfrac {1} {2}=\dfrac {AP} {AP +3}\)
 2\(\overline {AP}\) =  \(\overline {AP}\) + 3 \(\rightarrow\) AP = 3

Using Pythagorean theorem, you can get \(\overline {AE}\) = \(2\sqrt {2}\)
\(\Delta\) AEP is similar to \(\Delta\) ADC [This part is tricky. Make sure you see that !!]
 \(\rightarrow\) \(\dfrac {1} {\overline {DC}}=\dfrac {AE} {AD}\) = \(\dfrac {2\sqrt {2}} {8}\)
\(\overline {DC}\) = \(2\sqrt {2}\)  and \(\overline {BC}\) = 2 * \(2\sqrt {2}\) = \(4\sqrt {2}\)
The area of  \(\Delta\) ABC =  \(\dfrac{1}{2}\)*\(4\sqrt {2}\) * 8 =  \(16\sqrt {2}\)






Question: If you know the length of x and y, and the whole length of \(\overline {AB}\),

A: what is the ratio of a to b and 

B: what is the length of z.







Solution for question A:
\(\Delta\)ABC and \(\Delta\)AFE are similar so \(\dfrac {z} {x}=\dfrac {b} {a+b}\). -- equation 1
Cross multiply and you have z ( a + b ) = bx

\(\Delta\)BAD and \(\Delta\)BFE are similar so \(\dfrac {z} {y}=\dfrac {a} {a+b}\). -- equation 2
 Cross multiply and you have z ( a + b ) = ay

bx = ay so \(\dfrac {x} {y}=\dfrac {a} {b}\)  same ratio

Solution for question B: 
Continue with the previous two equations, if you add equation 1 and equation 2, you have:
\(\dfrac {z} {x}+\dfrac {z} {y}=\dfrac {b} {a+b}+\dfrac {a} {a+b}\)
\(\dfrac {zy+zx } {xy}=1\) \(\rightarrow\) z = \(\dfrac {xy} {x+y}\)




Applicable question: 

\(\overline {CD}=15\) and you know \(\overline {DB}:\overline {BC}=20:30=2:3\) 
 so  \(\overline {DB}=6\) and \(\overline {BC}=9\) 

\(\overline {AB}=\dfrac {20\times 30} {\left( 20+30\right) }\)= 12
↧

Triangular Numbers & Word Problems: Chapter Level

October 26, 2015, 6:47 pm
$
0
0
Triangular Numbers:  From Math is Fun. 1, 3, 6, 10, 15, 21, 28, 36, 45...

Interesting Triangular Number Patterns: From  Nrich

Another pattern: The sum of two consecutive triangular numbers is a square number.

What are triangular numbers? Let's exam the first 4 triangular numbers:

The 1st number is  "1".
The 2nd number is "3" (1 + 2)
The 3rd number is "6" (1 + 2 + 3)
The 4th number is "10" (1 + 2 + 3 + 4)
.
.
The nth number is \(\frac{n(n+1)}{2}\)

It's the same as finding out the sum of the first "n" natural numbers.

Let's look at this question based on the song "On the Twelve Day of Christmas"
(You can listen to this on Youtube,)

On the Twelve Day of Christmas
On the first day of Christmas
my true love gave to me
a Partridge in a Pear Tree

On the second day of Christmas,
My true love gave to me,
Two Turtle Doves,
And a Partridge in a Pear Tree.

On the third day of Christmas,
My true love gave to me,
Three French Hens,
Two Turtle Doves,
And a Partridge in a Pear Tree

On the fourth day of Christmas,
My true love gave to me,
Four Calling Birds,
Three French Hens,
Two Turtle Doves,
And a Partridge in a Pear Tree.


The question is "How many gifts were given out on the Day of Christmas?"

Solution I"
1st Day:       1
2nd Day:      1 + 2
3rd Day       1 + 2 + 3
4th Day        1 + 2 + 3 + 4
.
.
12th Day      1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12

Altogether, you'll have 12 * 1 + 11 * 2 + 10 * 3 + 9 * 4 + 8 * 5 + 7 * 6 + 6 * 7 + 5 * 8 + 4 * 9 + 3 * 10 + 2 * 11 + 1 * 12 = 12 + 22 + 30 + 36 + 40 + 42 + 42 + 40 + 36 + 30 + 22 + 12 = 364

Solution II: The sum of the "n" triangular number is a tetrahedral number.
To get the sum, you use \(\frac{n(n+1)(n+2)}{6}\)

n = 12 and \(\frac{12 (13)(14)}{6}= 364 \)

Here is a proof without words.

Another proof.

Applicable questions: (Answers and solutions below)

#1 Some numbers are both triangular as well as square numbers. What is the sum of the first three positive numbers that are both triangular numbers and square numbers?

#2 What is the 10th triangular number? What is the sum of the first 10 triangular numbers?

#3 What is the 20th triangular number?

#4 One chord can divide a circle into at most 2 regions, Two chords can divide a circle at most into 4 regions. Three chords can divide a circle into at most seven regions. What is the maximum number of regions that a circle can be divided into by 50 chords? 

#5: Following the pattern, how many triangles are there in the 15th image? 


















Answers: 
#1 1262  The first 3 positive square triangular numbers are: 1, 36 (n = 8) and 1225 (n = 49).

#255; 220   a. \(\frac{10*11}{2}=55\)  b. \(\frac{10*11*12}{6}=220\)

#3210   \(\frac{20*21}{2}=210\)  

#4 1276 
1 chord :    2 regions or \(\boxed{1}\) + 1
2 chords:   4 regions or  \(\boxed{1}\)  + 1 + 2
3 chords:   7 regions or \(\boxed{1}\)  + 1 + 2 + 3
.
.
50 chords:\(\boxed{1}\)  + 1 + 2 + 3 + ...+ 50 = 1 +  \(\frac{50*51}{2}\) =1276

#5: 120
The first image has just one triangle, The second three triangles. The third 6 triangles total. 
It follows the triangular number pattern. The 15th triangular is  \(\frac{15*16}{2}\) =120 

↧
↧

Mathcounts : Geometry -- Medians ; Squares in Isosceles Right Triangle, Similar Triangles, Triangles share the same vertex

November 10, 2015, 6:13 am
$
0
0
Check out Mathcounts here, the best competition math program for middle school students.
Download this year's Mathcounts handbook here.


















This one appears at 91 Mathcounts National Target #4. It's interesting.

Q: triangle ABC is equilateral and G is the midpoint. BI is the same length as BC and the question asks about the area of quadrilateral polygon GDBC.
We'll also find the area of triangle ADG and triagle DBI here. 

Solution I: The side length is 2 and it's an equilateral triangle so the area of triangle ABC is 
\(\dfrac {\sqrt {3}} {4}\times 2^{2}=\sqrt {3}\).
Using similar triangles GCF and ACE, you get \(\overline {GF}\)= \(\dfrac {\sqrt {3}} {2}\)
From there, you get area of  \(\Delta\)GIC = \(4*\dfrac {\sqrt {3}} {2}*\dfrac {1} {2}=\sqrt {3}\)
 \(\Delta\)FCH is a 30-60-90 degree right triangle so \(\overline {DH}=\sqrt {3}*\overline {BH}\)
Using similar triangles IDH and IGF, you get \(\dfrac {2+\overline {BH}} {3.5}=\dfrac {\sqrt {3}\overline {BH}} {\dfrac {\sqrt {3}} {2}}\) = 2\(\overline {BH}\);
2 +\(\overline {BH}\)= 7\(\overline {BH}\); \(\overline {BH}\)= \(\dfrac {1} {3}\)
\(\overline {DH}=\dfrac {\sqrt {3}} {3}\) = the height
 Area of \(\Delta\)DBI = 2 * \(\dfrac {\sqrt {3}} {3}\)*\(\dfrac {1} {2}\) = \(\dfrac {\sqrt {3}} {3}\)
Area of quadrilateral polygon GDBC =  \(\sqrt {3}-\dfrac {\sqrt {3}} {3}\)= \(\dfrac {2\sqrt {3}} {3}\)
The area of both  \(\Delta\)ABC and \(\Delta\)GIC is \(\sqrt {3}\) and both share the quadrilateral polygon GDBC (It's like a Venn diagram).
Thus, the area of both triangles are the same \(\dfrac {\sqrt {3}} {3}\).

Solution II:



There are some harder AMC-10 questions using the same technique.
Using triangles share the same vertex,  you get the two same area "a"s and "b"s because the length of the base is the same.
From the area we've found at solution I, we have two equations:
2a + b = \(\sqrt {3}\)
2b + a = \(\sqrt {3}\)
It's obvious a = b so you can find the area of the quadrilateral being the \(\dfrac {2} {3}\)of the equilateral triangle so the answer is \(\dfrac {2\sqrt {3}} {3}\).




Vinjai's solution III:

Draw the two extra lines and you can see that the three lines are medians, which break the largest triangle into 6 equal parts. [You can proof this using triangles share the same vertices : notes later.]
Quadrilateral polygon FECB is  \(\dfrac {2} {3}\)of the equilateral triangle so the answer is \(\dfrac {2\sqrt {3}} {3}\).







This is similar to 2005 Mathcounts National Target #4 questions. AMC might have similar ones.
Q:Both triangles are congruent and isosceles right triangles and each has a square embedded in it. If the area of the square on the left is 12 square unites, what is the area of the square on the right? 
Solution I: 


Solution II:
↧

2015 unofficial AMC 8 problems and detailed solutions

November 25, 2015, 3:23 pm
$
0
0
You know, the most amazing thing about various competitions are the energy, the pleasure, the spontaneity, the camaraderie and the kindred spirits.

Thanks a lot for those diligent, inquisitive boys and girls.

Below are their collaborated efforts.

You are one of its kind :)

2015 unofficial AMC 8 problems and detailed solutions from online whiz kids.

The official statistics will come up much, much later, so move on.

Thanks a lot for visiting my blog.

E-mail me at thelinscorner@gmail.com if you want to join us who LOVE problem solving (and many other areas equally challenging and engaging.)

Currently I'm running different levels of problem solving group lessons.Our first stop is AMC 8 and/or the SAT hardest problems prep (just for the very short term for a full ride scholarship).



↧

2013 Mathcounts School and Chapter Harder Problems

November 29, 2015, 7:09 am
$
0
0
You can now download and discuss with your friends this year's school and chapter problems.
Here is the link to the official Mathcounts website.

Some more challenging problems from this year's Mathcounts school/or chapter problems.

2013 school team #10 : Three concepts are testing here :
Hint: 
a. If you get rid of the remainder, the numbers will be evenly divided into 192, so you are looking at
those factors of 192 - 12 = 180

b. To leave a remainder of 12, those factors of 180 that are included in the Set must be smaller than 12, otherwise, you can further divide it.

c. To find the median, make sure to line up the numbers from the smallest to the largest and find the middle numbers. If there are even numbers of factors larger than 12, average the middle two. Otherwise, the middle number is the answer.



\(180=2^{2}\times 3^{2}\times 5 \) so there are (2 + 1) (2 + 1) (1 + 1) = 18 factors

The list on the left side gives you the first 9 and if you times those numbers with "5", you get 9 other factors,which are 5, 10, 20, 15, 18, 60, 45, 90 and 180.

Discard the factors that are smaller or equal to 12 and list all the other factors in order and find the median.

The answer is "36".



2013 Chapter Sprint:
#21: Dimensional change problem : The height of the top pyramid is \(\dfrac {2} {3}\) of the larger
pyramid so its volume is \(\left( \dfrac {2} {3}\right) ^{3}\) of the larger pyramid.

\(\left( \dfrac {2} {3}\right) ^{3}\times \dfrac {1} {3}\times \left( \dfrac {36} {4}\right) ^{2}\times 12
= \)\(96  cm^{3}\)

# 24:  According to the given:   \(xyz=720\)   and   \(2( xy+yz+zx)= 484 \) so
\(( xy+yz+zx )= 242\)

Since x, y and z are all integers, you factor 720 and see if it will come up with the same x, y and z values
for the second condition.

Problem writer(s) are very smart using this number because the numbers "6", "10", "12" would give you
a surface area of 252. (not right)

The three corrrect numbers are "8", "9", and "10" so the answer is \(\sqrt {8^{2}+9^{2}+10^{2}}=\) \(7\sqrt {5}\)

#25: Geometric probability: Explanations to similar questions and more practices below. 

Probability with geometry representations form Aops.

Geometric probability from "Cut the Knots".

#26:This one is similar to 2002 AMC-10B #21, so try that question to get more practices. 
2002 AMC-10B #21 link 

#27:
\(\dfrac {1} {A}+\dfrac {1} {B}=\dfrac {1} {2}\)
\(\dfrac {1} {B}+\dfrac {1} {C}=\dfrac {1} {3}\)
\(\dfrac {1} {C}+\dfrac {1} {A}=\dfrac {1} {4}\)
Add them up and you have  \(2 * (\dfrac {1} {A}+\dfrac {1} {B}+ \dfrac {1} {C})=\dfrac {13} {12}\)

\((\dfrac {1} {A}+\dfrac {1} {B}+ \dfrac {1} {C})=\dfrac {13} {24}\)

\(\dfrac {1} {\dfrac {1} {A}+\dfrac {1} {B}+\dfrac {1} {C}} = \)\(\dfrac {{24}} {13}\)hours

#28:Hint : the nth triangular number is the sum of the first "n" natural numbers and \(\dfrac {n\left( n+1\right) } {2}\) is how you use to find the sum.
From there, you should be able to find how many numbers will be evenly divided by "7".

#29 : Circle questions are very tricky so make sure to find more problems to practice accuracy.

#30 : 
Solution I: 
Read the solution that is provided by Mathcounts.org here.
Solution II:
Case 1 : \(x-1 > 0\rightarrow x > 1\) Times ( x - 1) on both sides and you have
\(x^{2}-1>8\) so x > 3 or x < -3 (discard)

Case 2: \(x-1 < 0\) so \(x < 1\) \(\rightarrow x^{2}-1 < 8\) [You need to change the sign since it's negative.]-3 < x < 3. Combined with x < 1 you have the range as -3 < x < 1
The answer is 60%.









                                               2013 Mathcounts Target #7 and 8: 

Target question #8 is very similar to 2011 chapter team #10. 
It just asks differently.   
Read the explanations provided on the Mathcounts official website.
They are explained very well.
Let me know if there are other easier ways to tackle those problems.

Hope this is helpful !! Thanks a lot !! Good luck on Mathcounts state.
↧
Search

2014 Mathcounts State Prep: Volume of a Regular Tetrahedron and Its Relationship with the Cube it's Embedded

December 14, 2015, 6:53 pm
$
0
0
How to find volume of a tetrahedron (right pyramid) with side length one.

The above link gives you a visual interpretation of the relationship of a regular tetrahedron, its
relationship with the cube that it is embedded and the other kind of tetrahedron (right angle pyramid).


The side of the cube is \(\dfrac {S} {\sqrt {2}}\) so the volume of the regular embedded tetrahedron is
\(\dfrac {1} {3}\times \left( \dfrac {S} {\sqrt {2}}\right) ^{3}\)=\(\dfrac {1} {3}*\dfrac {s^{3}} {2\sqrt {2}}\)= \(\dfrac {\sqrt {2}S^{3}} {12}\).

You can also fine the height of the tetrahedron and then \(\dfrac {1} {3}\)*base*space height to get the volume.
Using Pythagorean theory, the hypotenuse S and one leg which is \(\dfrac {2} {3}\) of the height of the equilateral triangle base, you'll get the space height.
↧
↧

Dimentional Change Questions III: Similar Shapes

December 17, 2015, 8:03 am
$
0
0
There are numerous similar triangle questions on Mathcounts.

Here are the basics:



If two triangles are similar, their corresponding angles are congruent and their corresponding sides will have the same ratio or proportion.

ΔABC and ΔDEF are similar. \(\frac{AB}{DE}\) = \(\frac{AC}{DF}\) = \(\frac{BC}{EF}\)= their height ratio = their perimeter ratio.







Once you know the linear ratio, you can just square the linear ratio to get the area ratio and cube the linear ratio to get the volume ratio. 

Practice Similarity of Triangles here.  Read the notes as well as work on the practice problems.  There is instant feedback online. 

Other practice sheets on Similar Triangles                                                        


Many students have trouble solving this problem when the two similar triangles are superimposed. 

Just make sure you are comparing smaller triangular base with larger triangular base and smaller triangular side with corresponding larger triangular side, etc... In this case:
\(\frac{BC}{DE}\)= \(\frac{AB}{AD}\) = \(\frac{AC}{AE}\)




Questions to ponder (Solutions below)


#1: Find the area ratio of Δ ABC to trapezoid BCDE to DEGF to FGIH. You can easily get those ratios using similar triangle properties. All the points are equally spaced and line \(\overline{BC}\)// \(\overline{DE}\) // \(\overline{FG}\) // \(\overline{HI}\). 



#2: Find the volume of the cone ABC to Frustum BCDE to DEGF to FGIH. Again, you can use the similar cone, dimensional change property to easily get those ratios.Same conditions as the previous question.

 



Answer key: 

#1:

 #2:


↧

Sequences and Series

December 29, 2015, 2:29 pm
↧

Mathcounts state/national level problems

January 11, 2016, 5:35 am
↧

For Mainly High School Students : Quest for USAJMO or USAMO

January 16, 2016, 10:04 am
$
0
0
↧
↧

2016 Mathcounts State Prep : How to Avoid Making Careless Mistakes

March 6, 2016, 2:47 pm
$
0
0
Why Can Some Kids Handle Pressure While Others Fall Apart? from the New York Times

Relax! You'll Be More Productive from the New York Times

First, please read Mathcounts "Forms of Answers" carefully for a few times and remind yourself not to write down the unallowable answers.

Stop Making Stupid Mistakes by Richard Rusczyk from Art of Problem Solving

How to Avoid Careless Mathematical Errors from Reddit

Common errors from all my students: 

Number 1 issue with most of the boys/and a few girls who have strong intuition in math is their horrible handwriting since their minds work much faster than their hands can handle. (See!! I'm making excuses for them.)

I call some of my students "second try ___ [Put your name here.] or third try ____ because I don't need to teach them how to solve a problem but the normal pattern is that it has to take them twice or three times to get it finally right. Thus, they need to slow down and organize their thoughts.

Practice your numbers:  4 (it's not 21), 7, 9 (don't dislocate the circle on top), 2 (don't make it looks like a 7), etc...  

35 cents is very different from 0.35 cents.

Unless stated, you write improper fraction as your answer. Make sure to simplify the answer.

Many mistakes happen when it involves fractions, negative numbers, parenthesis, and questions that
have radicals on the denominator and you need to simplify it, so make sure to double check your math.

Some problems takes many steps to reach the final solutions. Some involve lots of data, extreme long strings of information so if those are your weakness, skip them first and go back to them later.

Every point is the same so don't stay with a tedious question too long and panic later not able to finish the last few harder questions which might be much easier to solve arithmetic wise if you know how.

Circle questions trouble many students. Make sure you are aware of what's being tested.
Is it circumference or area, is it diameter or radius, is it linear to area (squared) or vice versa ?
Are the units the same (most frequently appeared errors)?

Don't forget to divide by 2 for the triangle, times 6 if you use area of an equilateral triangle to get the hexagon. For geometry questions or unit conversions, don't do busy work, write down the equivalent equations and cancel like crazy.

Same goes to probability questions, cancel, cancel and cancel those numbers. You don't need to practice mental math multiplication for most of the Mathcounts problems. Think Smart!!

The answer for probability questions can only be 0 to 1, inclusive.

For lots of algebra questions, manipulations are the way to go or number sense. Use the digit clue to help you narrow down the "trial and error" method. 

Make sure you have the terms and space type questions right. Calendar questions, how many numbers (inclusive, exclusive, between, ...), Stage doesn't necessarily start with 1 or 0.
Make sure you don't over-count or under-count.

Mos students got counting questions wrong when it involves limit.

Case in point : How many non-congruent triangles are there if the perimeter is 15? 
Answer: There are 7 of them.  Try it !!

To be continue...









↧

Mathcounts Strategy: Shoestring (or Shoelace) method of finding the area of any polygon

March 7, 2016, 6:07 am
$
0
0
Check out Mathcounts here, the best competition math program for middle school students.
Download this year's Mathcounts handbook here. 

Shoelace formula from Wikipedia

More on Shoelace

Problems: Solutions below 

#1:  Find the area of a quadrilateral polygon given the four end points (3, 5), (11, 4), (7,0) and (9,8) in a Cartesian plane.

#2 2007 Chapter Target Round: A quadrilateral in the plane has vertices at (1,3),  (1,1), (2, 1) and (2006, 2007). What is the area of the quadrilateral?

#3: Find the area of a polygon with coordinates (1, 1), (3, -1),  ( 4, 4), and  (0.3)

#4: What is the number of square units in the area of the pentagon whose vertices are 
(1, 1 ), ( 3, -1),  (6, 2), (5, 6), and (2, 5)?

#5: Find the area of a polygon with coordinates ( -6, 0), (0, 5), (3, -2), and (4, 7)

#6: Find the area of a polygon with coordinates (20, 0), (0, 12), (3, 0), (4, -4)

#7: Find the area of a polygon with coordinates (-8, 4), (2, 12), (3, -5), (4, -4)

#8: Find the area of a triangle with coordinate (-8, -4), (-3, 10), (5, 6)


















Solution I: Draw a rectangle and use the area of the rectangle minus the four triangles to get the area of the quadrilateral polygon. 








Solution II: Using shoestring method. First, plug in the four points. Second, choose one starting point and list the other points in order (either clockwise or counterclockwise)  and at the end, repeat the starting point. The answer is 33 square units.


























Use this link to practice finding the area of any irregular polygon. Keep in mind that a lot of the times you don't need to use shoestring method. Be flexible!! Scroll to the middle section.





#2 Answer: 3008 square units

#3: Answer:10.5 square units 

#4: Answer: 22 square units

#5: Answer: 45.5 square units

#6: Answer: 136 square units

#7: Answer: 98 square units

#8: Answer: 66 square units 
↧
Search

The Grid Technique in Solving Harder Mathcounts Counting Problems : from Vinjai

May 31, 2016, 2:15 pm
$
0
0


The following notes are from Vinjai, a student I met online. He graciously shares and offers the tips here on how to tackle those harder Mathcounts counting problems. 

The point of the grid is to create a bijection in a problem that makes it easier to solve. Since the grid just represents a combination, it can be adapted to work with any problem whose answer is a combination.

For example, take an instance of the classic 'stars and bars' problem (also known as 'balls and urns', 'sticks and stones', etc.):
Q: How many ways are there to pick an ordered triple (a, b, c) of nonnegative integers such that a+b+c = 8? (The answer is 10C2 or 45 ways.)
Solution I: 
This problem is traditionally solved by thinking of ordering 8 stars and 2 bars. An example is:
* * * |    | * * * * *
  ^       ^       ^
  a       b       c
This corresponds to a = 3, b = 0, c = 5.

Solution II: 
But this can also be done using the grid technique:




The red path corresponds to the same arrangement: a = 3, b = 0, c = 5. The increase corresponds to the value: a goes from 0 to 3 (that is an increase of 3), b goes from 3 to 3 (that is an increase of 0), and c goes from 3 to 8 (that is an increase of 5). So a = 3, b = 0, c = 5.

Likewise, using a clever 1-1 correspondence, you can map practically any problem with an answer of nCk to fit the grid method. The major advantage of this is that it is an easier way to think about the problem (just like the example I gave may be easier to follow than the original stars and bars approach, and the example I gave in class with the dice can also be thought of in a more numerical sense).

↧

2013 Mathcounts Natinals Sprint # 28

June 1, 2016, 7:55 pm
$
0
0

2013 Mathcounts National Sprint #28 : In right triangle ABC, shown here,  line AC = 5 units and line BC = 12 units. Points D and E lie on  line AB and line BC respectively, so that line CD is perpendicular to line AB and E is the midpoint of line BC. Segments AE and CD intercept at point F. What is the ratio of AF to FE ? Express your answer as a common fraction.

                                                     Solution I : Using similar triangles



                                                        Solution II : Use Mass Point Geometry
↧
↧

Mathcounts Prep : Algebra Manipulation

July 6, 2016, 1:53 pm
$
0
0
Note that: 

\(\left( x+y\right) ^{2}-2xy= x^{2}+y^{2}\)
\(\left( x-y\right) ^{2}+2xy= x^{2}+y^{2}\)
\(\left(x-y\right) ^{3}+3xy\left( x-y\right) =x^{3}-y^{3}\)
\(\left( x+y\right) ^{3}-3xy\left( x+y\right) =x^3 + y^{3}\)
\(\left( x+y+z\right) ^{2}-2\left( xy+yz+xz\right) =x^{2}+y^{2}+z^{2}\)

Applicable questions:

Question 1: If x + y = a and xy = b, what is the sum of the reciprocals of x and y?

Solution: 
\(\dfrac {1} {x }+\dfrac {1} {y}=\dfrac {x +y} {xy}\)= \(\dfrac {a} {b}\)

Question 2: If \(x^{2}+y^{2}=153\) and x + y = 15, what is xy?

Solution: 
\(\left( x+y\right) ^{2}-2xy= x^{2}+y^{2}\)
\(15^{2}-2xy=153\)\(\rightarrow xy=36\)

Question 3: If \(\left( x+y\right) ^{2}=1024\) , \(x^{2}+y^{2}\) = 530 and x > y , what is x - y? 

Solution: 
 \(\left( x+y\right) ^{2}-2xy=x^{2}+y^{2}\)
1024 - 2xy = 530\(\rightarrow 2xy=494\)
\(\left( x-y\right) ^{2}+2xy=x^{2}+y^{2}\)
\(\left( x-y\right) ^{2}=36\)
x - y = 6

Question 4: x + y = 3 and  \(x^{2}+y^{2}=89\), what is \(x^{3}+y^{3}\)? 

Solution: 
\(\left( x +y\right) ^{2}-2xy=x^{2}+y^{2}\)
9 - 2xy = 89 \(\rightarrow -2xy=80\) so xy = -40
\(\left( x+y\right) ^{3}-3xy\left( x+y\right) =27 - 3(-40)* 3 = 27 + 3*40*3 = x ^{3}+y^{3}\)
\(x ^{3}+y^{3}\)= 387

Question #5: If \(x+\dfrac {1} {x}=5\), what is \(x^{3}+\dfrac {1} {x ^{3}}\)?

Solution:
\(\left( x+\dfrac {1} {x}\right) ^{3}=x^{3}+3x^{2}.\dfrac {1} {x}+3x.\dfrac {1} {x^{2}}+\dfrac {1} {x^{3}}\)
\(5^{3}=x^{3}+3\left( x+\dfrac {1} {x}\right) +\dfrac {1} {x^{3}}\)
125 - 3*5 = \(x^{3}+\dfrac {1} {x ^{3}}\)
The answer is 110.

Question #6 : 2011 Mathcounts state sprint #24 : x + y + z = 7 and \(x^{2}+y^{2}+z^{2}=19\), what is the arithmetic mean of the three product xy + yz + xz? 

Solution: 
\(\left( x+y+z\right) ^{2}-2\left( xy+yz+xz\right) =x^{2}+y^{2}+z^{2}\)
\(7^{2}-2\left( xy+yz+xz\right) =19\)
xy + yz + xz = 15  so their mean is \(\dfrac {15} {3}=5\)



More practice problems (answer key below):

#1:If x + y = 5 and xy = 3, find the value of \(\dfrac {1} {x^{2}}+\dfrac {1} {y^{2}}\). 

#2: If x + y = 3 and \(x^{2}+y^{2}=6\), what is the value of \(x^{3}+y^{3}\)? 

#3: The sum of two numbers is 2. The product of the same two numbers is 5. 
 Find the sum of the reciprocals of these two numbers, and express it in simplest form. 

#4:If \(x-\dfrac {6} {x}\) = 11, find the value of \(x^{3}-\dfrac {216} {x^{3}}\)? 

#5: If \(x+\dfrac {3} {x} = 9\), find the value of \(x^{3}+\dfrac {27} {x^{3}}\)?

#6:If \(x+\dfrac {1} {x} = 8\), what is \(x^{3}+\dfrac {1} {x ^{3}}\)? 





Answers:
#1 :\(\dfrac {19} {9}\)
#2: 13.5
#3: \(\dfrac {2} {5}\)
#4: 1529 [ \(11^{3}\)+ 3 x 6 x 11 =1529]
#5: 648   [\(9^{3}\)-3 x 3 x 9 = 648]
#6: 488   [ \(8^{3}\)– 3 x 8 = 488]
↧

2015 Mathcounts State/National Prep

January 26, 2015, 8:44 am
$
0
0
Harder concepts from Mathcounts Mini :
Also try the follow-up problems with detailed solutions. Don't do every question. Just the ones you think is hard.

Geometry :
#27 : Area and Volume 

#30: Similar Triangles and Proportional Reasoning

#34: Circles and Right Triangles

#35: Using Similarity to Solve Geometry Problems

#41: Analytic Geometry : Center of Rotation

More questions to practice from my blog post. 

From Mathcounts Mini : Video tutorials on counting and probability for Mathcounts state/national prep concepts are in the of difficulty.

Counting the Number of Subsets of a Set

Constructive Counting

More Constructive Counting 

Probability and Counting

Probability with Geometry Representations  : Oh dear, the second half part is hilarious.

Probability with Geometry Representations : solution to the second half problem from previous video

Try this one from 1998 AIME #9. It's not too bad.

From Mathcounts Mink : Center of rotation, equal distance from a point to other two points or two lines, angle bisector (last problem on the follow-up worksheet)

Mathcounts Mini : #41 - Analytic Geometry
↧

2015 Mathcounts State Prep: Simon's Favorite Factoring Trick

March 16, 2015, 11:21 am
$
0
0
Check out Mathcounts here, the best competition math program for middle school students.
Download this year's Mathcounts handbook here.

The most common cases of Simon's Favorite Factoring Trick are:

I:  \(xy+x+y+1=\left( x+1\right) \left( y+1\right)\)

II:  \(xy-x-y+1=\left( x-1\right) \left( y-1\right)\)

It's easy to learn. Here is the best tutorial online, by none other than Richard Rusczyk.
The method Rusczyk uses at the second half is very nifty. Thanks!!

Questions to ponder:(answer key below)
#1: Both x and y are positive integers and \(x>y\). Find all positive integer(s) that \(xy+x+y=13\) 
#2: Both x and y are positive integers and \(x>y\). Find all positive integer(s) that \(2xy+2x-3y=18\)
#3: Find the length and the width of a rectangle whose area is equal to its perimeter.
#4: Twice the area of a non-square rectangle equals triple it's perimeter, what is the area of the rectangle? 













Answer key:
#1: x = 6 and y = 1
#2: ( x, y ) = (4, 2) 
#3: Don't forget square is a kind of rectangle (but not the other way around) so there are two answers: 
4 by 4 and 3 by 6 units. 
#4: One side is 4 units and the other 12 units so the answer is 4 x 12 or 48 square units. 
There is another one, 6 by 6 that would fit if the question doesn't specify non-square rectangle. 
↧
Viewing all 242 articles
Browse latest View live
Search